Optymalizacja zapasów przy planowaniu produkcji

Za pomocą modeli planowania zapasów można opty­malizować długości serii w procesie produkcyjnym, jednak w tym przypadku trzeba również zaprognozować popyt na produkowany wyrób gotowy. Popyt na wytwarzany wyrób jednocześnie wpływa na zapotrzebowanie na odpowiednie su­rowce niezbędne w procesie produkcyjnym.

Optymalizację długości serii w procesie produkcyjnym można prześledzić na poniższym przykładzie. Firma zamierza produ­kować nowy wyrób. W celu uruchomienia produkcji jednej se­rii nowego wyrobu musi ponieść określone koszty stałe (niezwiązane z ilością produkowanych wyrobów w danej serii), jak koszty przezbrojenia maszyn i urządzeń na linii produkcyjnej, koszty związane z organizacją procesu produkcyjnego, koszty zamówień dostaw surowca itp.

Oszacowany koszt przygotowania produkcji jednej serii tego wyrobu wynosi 17.500 zł. Zakładany popyt w skali 1 roku to 180 000 sztuk. Zakładamy, że sprzedaż będzie kształtować się w sposób równomierny. Jednostkowy koszt utrzymania zapasu wyprodukowanego wyrobu wynosi 1,75 zł. Obliczamy:

• optymalną długość serii,
• liczbę serii,
• łączny koszt związany z przygotowaniem produkcji,
• łączny koszt utrzymania zapasu wyrobu.

Aby to przeliczyć, można posłużyć się modelem Wilsona, dokonawszy odpowiedniej jego modyfikacji. Obecnie mamy do czynienia z kosztem przygotowania produkcji danej serii – jest to koszt niezależny od ilości wyprodukowanych wyrobów. Natomiast w problemie optymalizacyjnym nie występuje koszt zamówienia dostaw surowca – koszt ten ujęty jest w koszcie przygotowania produkcji. Stąd posługujemy się wzorem:

S =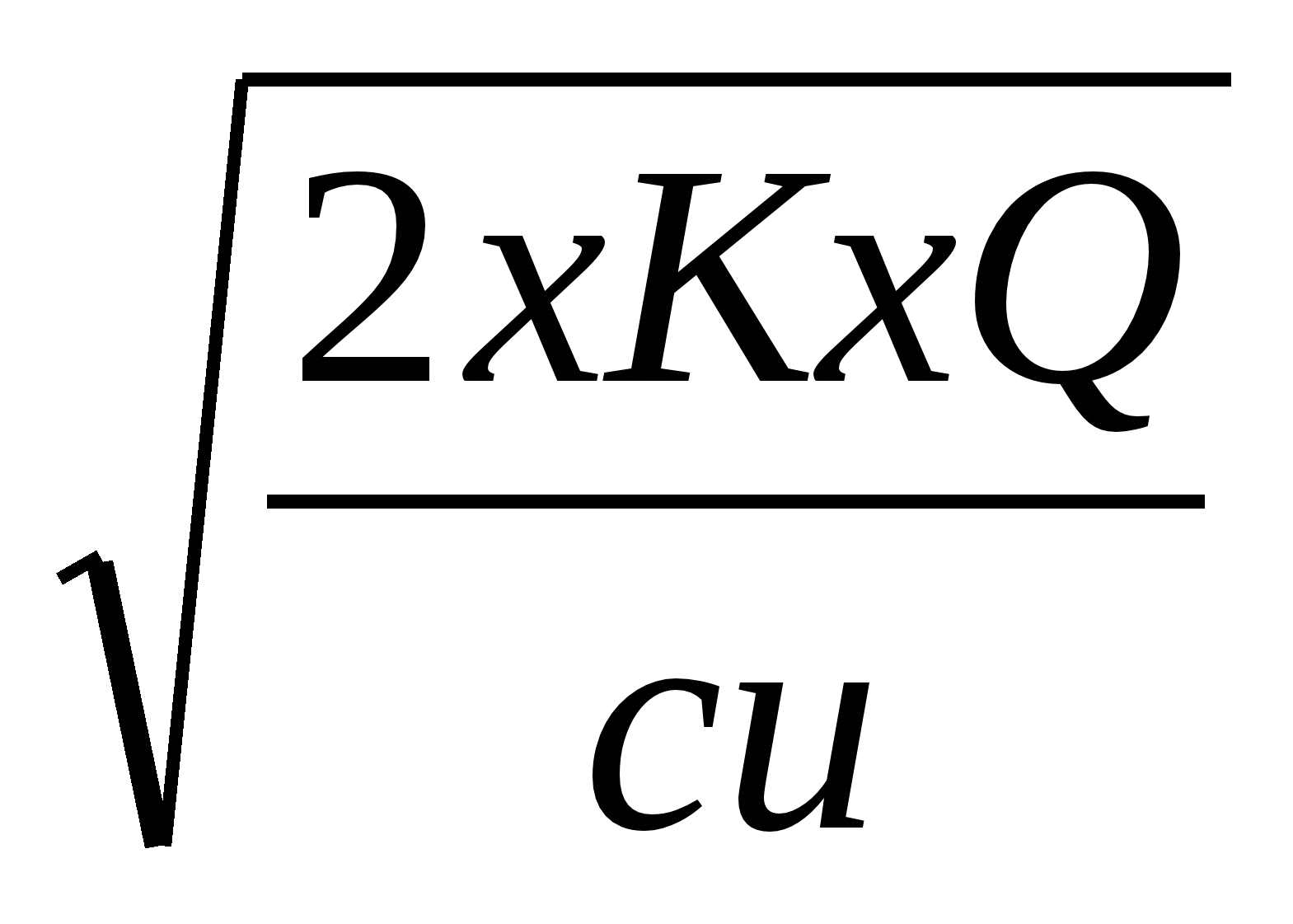

K – koszt przygotowania produkcji danej serii

a) optymalną długość serii (d_s):

d_s = = 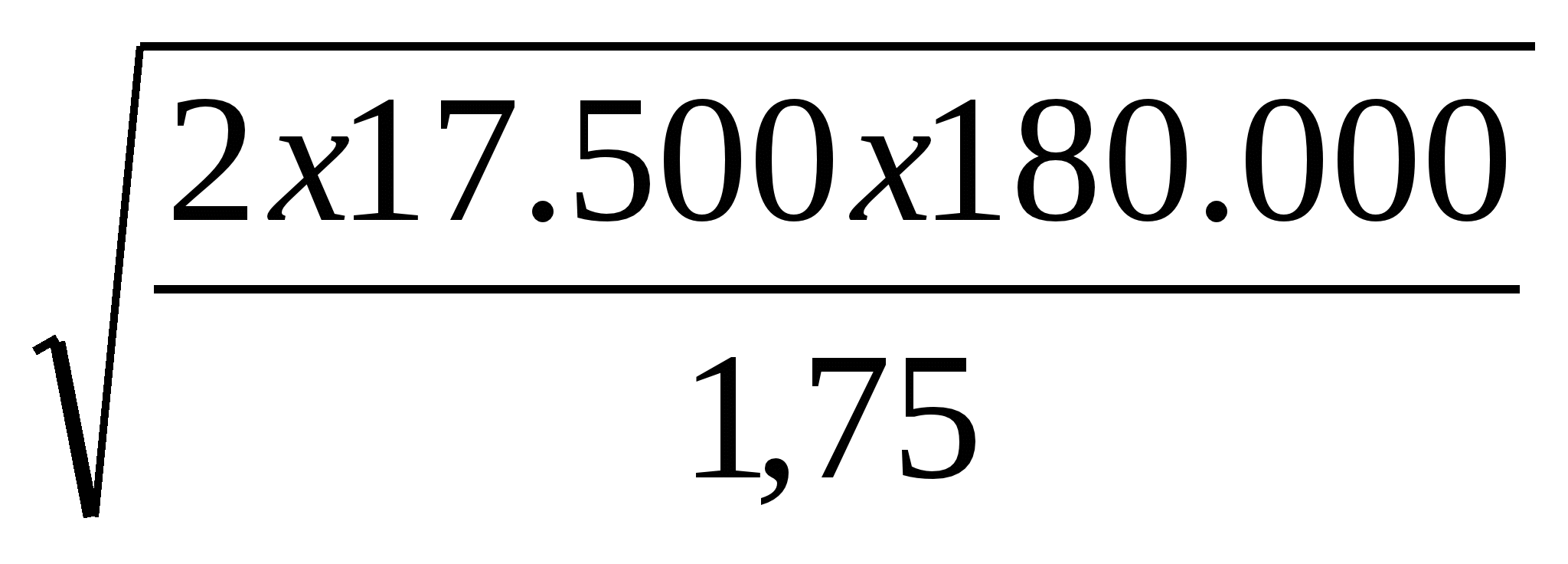= 60.000

b) liczba serii:

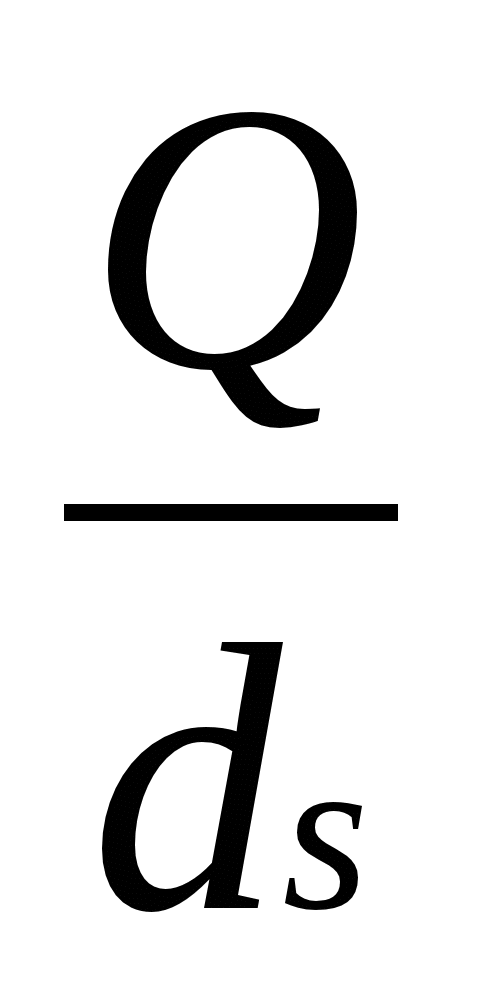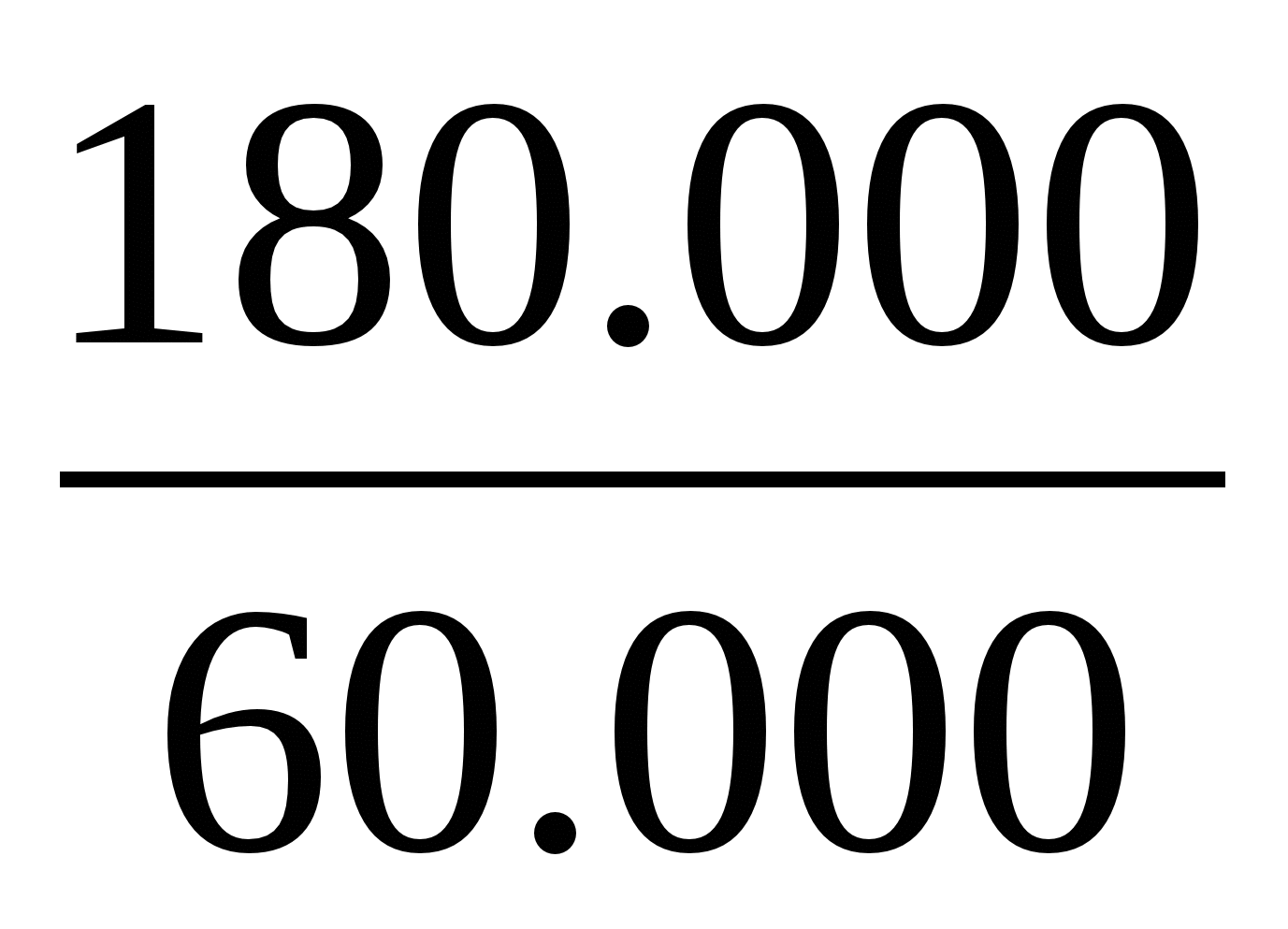n = = = 3

c) łączny koszt związany z przygotowaniem produkcji:

P_R = K x n = K x Q/ d_s = 17.500 x 180.000 / 60.000 = 52.500 zł

d) łączny koszt utrzymania zapasu wyrobu:

D_U = Cu x d_s / 2 = 1,75 x 60.000 / 2 = 52.500

Łączne koszty ogółem przygotowania produkcji i utrzymy­wania zapasu wyrobów gotowych wynoszą 52.500 + 52.500 = = 105.000 zł.

Omówione powyżej deterministyczne modele planowania zapasów stanowią zaledwie bardzo niewielki odsetek znanych w teorii i praktyce tego rodzaju modeli. Modele te można dalej rozwijać, uzupełniać lub wprowadzać nowe założenia. Przykładowo poluźnienie założenia o równomiernym zużyciu zaso­bu w przypadku sezonowości produkcji czy też wprowadzenie nowego założe­nia o sezonowości dostaw danego zasobu. Oba przypadki spotyka się choćby w przedsiębiorstwach przetwórstwa warzyw i owoców.

Można również skorzystać z tzw. modeli probabilistycznych, które są stosowane w przypadkach, gdy zapotrzebowanie na dany surowiec jest nieznane i wobec tego ma charakter losowy. Tego rodzaju modele zapasów można wykorzystać do optyma­lizacji gospodarki magazynowej przedsiębiorstwa handlowego, szczególnie firm zajmujących się handlem wysyłkowym na szeroką skalę.